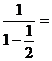Soluzioni dei giochi matematici

Infatti, se si indica con x il numero pensato si ha l'identità:

{[(2x + 5) 5 + 10] 10 – 350} : 100 = x

Per determinare il giorno della settimana corrispondente ad una certa data, ad es. al 30 aprile 1777, si può seguire il seguente procedimento pubblicato dal matematico Zeller negli « Acta Mathematica » di Stoccolma del 1887.

Calcoliamo i valori dei due numeri S ed R dati dalle due formule:

in cui g indica il giorno del mese, m il numero d'ordine del mese, A l'anno ed inoltre intendendo che, nelle divisioni indicate dalle frazioni, bisogna considerare solo le parti intere dei quozienti. Applicando queste due formule si ha quindi:

Calcoliamo ora la differenza S – R; si ha:

S – R = 2262 – 11 = 2251

La differenza si divide per 7 e si considera il resto di questa divisione. Esso indica il giorno della settimana corrispondente alla data considerata: se è 0 il giorno è sabato, se è 1 domenica, se 2 lunedì, ecc. Nel nostro caso, quindi, essendo quel resto 4, esso indica che il 30 aprile 1777 fu mercoledì. Non è semplice e nello stesso tempo meraviglioso?

Nell'applicare questo procedimento, si tenga però presente che i mesi di gennaio e febbraio debbono essere considerati rispettivamente come il 13° ed il 14° mese dell'anno precedente.

Inoltre, questo procedimento è valido per il calendario gregoriano (che è quello attualmente in uso; adottato dal 15 ottobre 1582, nei paesi cattolici) se si vuole applicarlo ad una data del calendario giuliano (che ha preceduto quello gregoriano e vale dal 1° gennaio dell'anno 45 a. C.) bisogna considerare R = 0.

Il risultato,  solo apparentemente paradossale, dipende dal fatto che , per cui l’arabo non aveva destinato ai suoi figli tutti i 17 cammelli, ma solo i  di essi. Eseguendo alla lettera la  volontà dell'arabo sarebbe quindi rimasto dell'eredità, cioè  di cammello, non distribuito. E sono proprio questi  di cammello che distribuiti fra i tre figli permettono che ciascuno di essi riceva un numero intero di cammelli e tuttavia più di quanto aveva stabilito il loro padre.

Il problema si può risolvere in modo semplicissimo, con la sola aritmetica, mediante il seguente ragionamento.

Ogni due salti il cane percorre 5,95 metri e nello stesso tempo il coniglio, che fa tre salti, percorre 4,95 metri; dunque in ciascuno di quegli intervalli di tempo (in cui il cane fa due salti ed il coniglio tre) il cane guadagna 1 metro sul coniglio. E poiché la distanza che divide il cane dal coniglio è di 6 metri, è evidente che il cane raggiungerà il coniglio quando saranno passati 6 di quegli intervalli di tempo, cioè quando il coniglio avrà percorso 29,70 metri (6 x 4,95) e quindi alla distanza di 10,30 metri (40 – 29,70) dalla tana.

Calcoliamo il percorso compiuto dalla mosca nel suo primo  volo, per andare dal primo bue al secondo. Quando la mosca ha incontrato il secondo bue è evidente che bue e mosca hanno percorso tutta la strada, cioè 10 km; ma poiché la mosca ha velocità tripla di quella del bue, essa avrà percorso i di 10 km ed il bue .

Nell'istante in cui la mosca incontra il secondo bue (che ha percorso  di 10 km), anche il primo bue ha percorso di   10   km  e quindi la distanza dei due buoi è diventata  . Ora la mosca ritorna dal primo bue e quando lo incontra avrà percorso, per lo stesso ragionamento di prima, i  della distanza fra i due buoi, cioè .

Così continuando, si ha quindi che le lunghezze dei successivi voli compiuti dalla mosca sono date da:

                                                         ..…

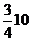
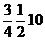
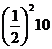
Calcoliamone la somma:

 

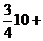
Cioè:

Fra parentesi c'è la somma degli infiniti termini di una progressione geometrica di ragione . Essa è eguale a

.   Quindi la lunghezza del percorso compiuto dalla mosca è data da: 

Tutto va bene, però... si può anche risolvere il problema molto più semplicemente, senza fare alcun calcolo. In che modo?

Soluzione «semplice» del «Problema della mosca»

Basta osservare che i due buoi s'incontrano a metà strada, ossia dopo un'ora di cammino, e quindi la mosca, che ha volato ininterrottamente alla velocità di 15 km/ora, ha percorso proprio 15 km.

Anzitutto, si tenga presente che una persona può avere al massimo 120.000 capelli. Quindi i primi 120.000 abitanti di Roma possono avere un numero di capelli l'uno diverso dall'altro; però, considerando un secondo gruppo di 120.000 abitanti, anche se questi hanno ciascuno un numero di capelli diverso da tutti gli altri, ne avremo già due (uno del primo gruppo e l'altro del secondo) che hanno ugual numero di capelli. Così continuando il ragionamento per tutti i 22 gruppi, di 120.000 abitanti ciascuno, che possono formarsi con tutti gli abitanti di Roma, che sono 2.650.000 (censimento 2001), se ne deduce che vi sono almeno 22 abitanti che hanno lo stesso numero di capelli.

Ecco un esempio semplice di come il ragionamento matematico permetta di risolvere una questione apparentemente strana ed insolubile.

Indicando con x il numero delle cartoline comprate da uno dei due padri (e quindi anche il costo di ciascuna di queste cartoline) e con y il numero delle cartoline comprate dal figlio (e quindi anche il costo di ciascuna di queste cartoline), la spesa del padre è di x ∙ x (cioè x²) euro e quella del figlio di y ∙ y (cioè y²) euro.

E poiché ogni padre spende 15 euro di più del proprio figlio, si deve avere:

x²  - y² = 15

Quest'equazione, in due incognite, è indeterminata; ma, tenuto conto che i valori di x ed y debbono essere numeri interi, perché siano accettabili come soluzioni del problema, le uniche soluzioni accettabili sono:

      

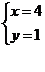
E poiché sappiamo che Giacomo (che è un figlio) compra 3 cartoline di più di Luigi (che è un padre), dall'esame delle due soluzioni sopra scritte deduciamo che Giacomo è quello che ha comprato 7 cartoline e Luigi il padre che ne ha comperato 4. Di conseguenza è Andrea (l'altro figlio) che ha comprato 1 cartolina e Pietro (l'altro padre) che ne ha comprato 8.

Ma il padre di Andrea, che ha comprato 1 cartolina, è quello che ha comprato 4 cartoline e quindi è Luigi.

Indicando con g il giorno del mese in cui è nato l'amico, con m il numero d'ordine del mese e con e l'età che l'amico compie nell'anno in corso, le operazioni che l'amico è stato invitato a compiere danno i seguenti risultati:

1°)       (2g + 11)50 = 100g + 550

2°)       [(100g + 550 + m)2 + 11]50 - 10.000g + 100m + 55.550

3°)       10.000g+100m+55.550 –e+60=10.000g+100m+55.610– e

Dunque, l'ultimo risultato ottenuto è:

10.000g + 100m + 55.610 - e

Togliendo da questo numero 55.555 si ha:

10.000g + 100m + 55.610 – e – 55.555  

Cioè:

10.000g + 100m + 55 – e

Questo è il numero finale ottenuto e la forma in cui esso è scritto dice appunto che, diviso in gruppi di due cifre ciascuno, il 1° gruppo a sinistra indica il giorno, il 2° gruppo il mese ed il 3° le ultime due cifre di destra dell'anno di nascita.

Se volete contattarci cliccate qui

(Se qualcosa fosse protetta da copyright segnalatecelo e noi provvederemo ad eliminarlo)